

 |

|
Bitte beachte die Copyrighthinweise.
Serien- und Parallelresonanz
Aufgabenstellung
· Messung der Spannungen und des Stroms an einer Serienschaltung von R-L-C über die Frequenz.
· Messung der Spannung und der Ströme an einer Parallelschaltung von R-L-C über die Frequenz.
· Messung an einem gedämpften Schwingkreis.
1 Allgemeines
Vor der Messung wurden die Tastköpfe abgeglichen, die Verbindungen wurden gelötet.
Als Eingangsspannungen wurden immer Sinussignale verwendet.
Als Kondensator wurde bei allen Messungen ein C = 150nF verwendet.
Als Widerstand wurde zuerst ein 1kW-Widerstand verwendet. Bei einem zu kleinen Widerstand würde der Funktionsgenerator (Ri=50W) zu stark belastet werden, bei einem zu großen wäre kein so deutliches Verhalten der Spannungen zu erkennen. Bei der Serienschaltung trat dieser zweite Fall auf, weshalb der Widerstand gleich auf 470W, genauer (mit Multimeter P2 gemessen) auf R = 468W reduziert wurde.
Der Wert der Spule wurde im Verlauf der Messung errechnet, der Kupferwiderstand betrug 1,9W (mit Multimeter P2 gemessen).
2 Serienschaltung
2.1 Schaltung
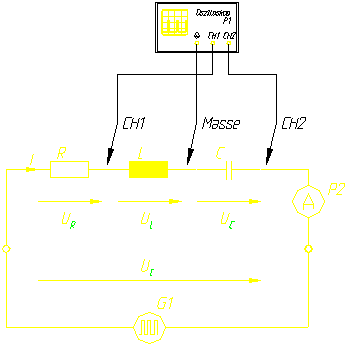
R=470 (468) W
C=150nF
L=14,6mH (errechnet)
2.2 Messung
Zuerst wurde die Resonanzfrequenz des Systems ermittelt. Dies ist dann der Fall, wenn der Imaginärteil der Eingangsspannung null wird, d.h. die Phase j ebenfalls null ist, oder wenn die Beträge der Spannungen an der Spule und an dem Kondensator gleich sind. Hier wurde die letztere Methode verwendet: Die Frequenz der Eingangsspannung wurde solange verändert, bis die Spannungen UCss und ULss gleich waren.
Als Eingangsspannung wurden Uess=5V verwendet und konstant gehalten.
2.2.1 Meßwerte
|
f [kHz] |
UCss [V] |
ULss [V] |
Ieff [mA] |
|
3,125 |
2,0 |
2,0 |
2,46 |
|
0,1 |
4,9 |
» 0 |
0,23 |
|
1,0 |
4,25 |
0,6 |
1,77 |
|
1,5 |
3,9 |
0,83 |
2,00 |
|
2,0 |
3,4 |
1,2 |
2,32 |
|
2,5 |
2,7 |
1,55 |
2,45 |
|
3 |
2,2 |
1,9 |
2,47 |
|
3,5 |
1,65 |
2,2 |
2,40 |
|
4 |
1,2 |
2,4 |
2,27 |
|
5 |
0,75 |
2,55 |
2,01 |
|
10 |
1,25 |
2,9 |
1,06 |
|
20 |
1,75 |
2,65 |
0,29 |
|
100 |
2,4 |
1,4 |
0 |
|
200 |
3,1 |
0,9 |
0 |
2.2.2 2.2.3 Berechnung von XC, XL, Z
Aus der Messung kann man XC, XL und Zges berechnen. Im Diagramm würde sich für XC ein x-1 Verlauf, für XL etwa Gerade und für Zges=XC+XL+R eine Kurve mit einem Minimum bei Resonanz ergeben.
Rein Lehrbuchmäßig ergibt sich
für XC (=XL) z.B. bei f = 3125Hz:![]() =339W
=339W
Laut der Messung beträgt XC aber:
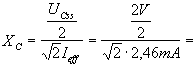 287W
287W
2.2.4 Berechnung von L
Aus der Thomsonschen Schwingungsformel wurde die Induktivität errechnet:
L = (wr2·C)-1 =(2·p·3125Hz·150nF)-1 = 17,3mH
Die Berechnung über XL=287W
ergibt: L ![]() 14,6mH
14,6mH
2.2.5 Berechnung der Güte
Die Güte ergibt sich zu (es wurden die Spitzenwerte verwendet):
![]()
2.2.6 Diagramm
Diagramm Serie
3 Serienschaltung
3.1 Schaltung
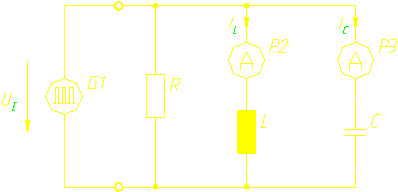
R=470 (468) W
C=150nF
L=14,6mH (errechnet)
3.2 Messung
Zuerst wurde die Resonanzfrequenz des Systems ermittelt (vergl. Serienschaltung). Die Frequenz der Eingangsspannung wurde solange verändert, bis die Ströme ICeff und ILeff gleich waren.
Als Eingangsspannung wurden Uess=5V verwendet und konstant gehalten, lediglich bei geringen Frequenzen brach die Spannung ein (Spule).
3.2.1 Meßwerte
|
f [kHz] |
ICeff [mA] |
ILeff [mA] |
UEss [V] |
|
3,100 |
4,97 |
4,97 |
5,0 |
|
0,1 |
0,068 |
47,2 |
2,8 |
|
1,0 |
1,49 |
11,77 |
|
|
1,5 |
2,55 |
8,36 |
|
|
2,0 |
3,26 |
7,03 |
|
|
2,5 |
3,93 |
5,89 |
|
|
3 |
4,85 |
4,94 |
5,0 V |
|
3,5 |
5,76 |
4,39 |
geregelt |
|
4 |
6,35 |
3,72 |
|
|
5 |
7,71 |
3,09 |
|
|
10 |
15,14 |
1,50 |
|
|
20 |
26,0 |
0,48 |
|
|
100 |
21,3 |
0,0123 |
3.2.2 Berechnung der Güte
Bei Uess von 5V ergibt sich ein Effektivwert von 1,77V, der bei einem Widerstand von 486W einen Strom von 3,7mA durch den Widerstand zur Folge hat und den Gesamtstrom darstellt, da sich IC und IL aufheben.
![]()
3.2.3 Diagramm
Diagramm parallel
4 Gedämpfter Schwingkreis
4.1 Schaltung
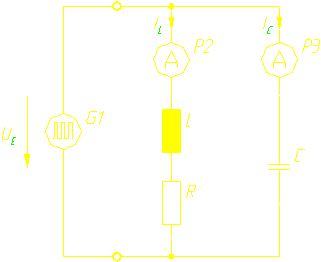
R=470 (468) W
C=150nF
L=14,6mH (errechnet)
4.2 Messung
Zuerst wurde die Resonanzfrequenz des Systems ermittelt (vergl. Serienschaltung). Die Frequenz der Eingangsspannung wurde solange verändert, bis die Ströme ICeff und ILeff gleich waren.
4.2.1 Meßwerte
|
f [kHz] |
ICeff [mA] |
ILeff [mA] |
UEss [V] |
|
2083 |
4,25 |
4,25 |
6,8 |
Bei dieser Resonanzfrequenz handelt es sich um die normale Resonanzfrequenz. Die Eigenfrequenz (Impuls) wurde nicht mehr gemessen.
4.2.2 Berechnung der Resonanzfrequenz:
Laut Theorie ergibt sich:
![]() , dies führt jedoch
zu einer komplexen Lösung :-(
, dies führt jedoch
zu einer komplexen Lösung :-(
5 Interpretation der Meßergebnisse
Bis etwa 5kHz zeigten die Schaltungen die erwarteten Eigenschaften.
Darüber trat bei der Serienschaltung eine Erhöhung der Kondensatorspannung auf, die eigentlich gegen 0V gehen sollte, während die Spannung an der Spule wieder abnimmt d.h. die Spule zeigt Eigenschaften eines Kondensators und umgekehrt. Der Strom hat bei der Resonanz ein Maximum.
Bei der Parallelschaltung verläuft der Spulenstrom wie erwartet, während der Strom durch den Kondensator ein Plato bildet (Spulenverhalten).
Das Verhalten der Bauteile im hohen Frequenzbereich kann dadurch erklärt werden, daß es sich nicht um ideale Bauelemente handelt.
Da der Strom mit Multimetern gemessen wurde, ist die Messung über 10kHz nicht mehr ganz genau.
Erwähnenswert ist die gute Übereinstimmung der Resonanzfrequenzen bei der Serienschaltung und der Parallelschaltung, da dies nicht unbedingt der Fall sein muß, obwohl überall die Thomsonsche Schwingungsformel gilt.
Bei der rechnerischen Ermittlung von L ist eine geringe Differenz zwischen den beiden Berechnungen (Thomson, XL) vorhanden. Hier ist der Wert, der aus XL errechnet wurde, sicher genauer, da bei der Resonanzfrequenz zwei Probleme auftreten: die Messung von fr ist nicht ganz exakt und der Kondensator ist toleranzbehaftet.
